
|

|
|
Menu
Email : larmesblanches@larmesblanches.com |
La méthode du SimplexeProgrammation linéaire par l'algorithme de DantzigIl s'agit de déterminer un maximum en fonction de contraintes économiques, par exemple
un profit. 2/ Transformer les inéquations de contrainte en équations Introduire des variables d'écart. Il y a autant de variables d'écart que d'inéquations de contrainte. 3/ Mettre en forme matricielle : Base de départ 2 ) Traitement itératif Répéter les opérations suivantes jusqu'à ce que tous les coefficients de la fonction économique soient nuls ou négatifs. 1/ Choisir la variable de la colonne pivot C'est la variable dont le coefficient de la fonction économique est le plus grand 2/ Déterminer la variable de la ligne pivot Faire ligne par ligne le rapport du 2 membre avec le coefficient de la variable pivot située sur la même ligne. La variable de la ligne pivot est celle dont le coefficient différent de 0 appartient à la ligne pour lequel le rapport est le plus petit et > 0. 3/ Confectionner le nouveau tableau L'intersection de la ligne pivot avec la colonne pivot détermine la case pivot. Les transformations du tableau sont les suivantes : b/ Ligne pivot : diviser tous les coefficients par la valeur du pivot. Le pivot prend donc la valeur 1. c/ Colonne pivot : Mettre à 0 les coefficients de la colonne pivot, excepté le pivot qui reste à la valeur 1. d/ Pour les autres valeurs du tableau procéder comme suit à partir du tableau précédent : 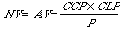 Avec : NV : Nouvelle Valeur de la case considérée du tableau AV : Ancienne Valeur de la case considérée du tableau CCP : Coefficient précédent de la colonne pivot situé sur la même ligne que AV CLP : Coefficient précédent de la ligne pivot situé sur la même Colonne que AV P : Valeur précédente du pivot. Fin de répéter Après la dernière itération, les résultats se trouvent dans la colonne des seconds membres. Attention : il faut changer le signe du second membre de la fonction économique.  Tableau n 2  En savoir plus :
Optimisation
En savoir plus :
Optimisation
|